Cálculo de la fuerza de flexión durante la flexión libre de la máquina dobladora de chapa

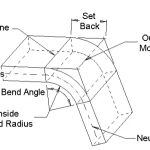
En los últimos años, las máquinas dobladoras de frenos de metal se han utilizado ampliamente en varias industrias, y el rango de procesamiento de las máquinas dobladoras se ha expandido. Sin embargo, no ha habido una discusión sistemática sobre el cálculo de la fuerza de flexión. En la actualidad, hay aproximadamente dos tipos de fórmulas de cálculo de la fuerza de flexión recomendadas en los manuales de varios fabricantes de máquinas plegadoras de plegadoras.

P - fuerza de flexión, KN;

S - espesor de la hoja, mm;

l - la longitud de flexión de la hoja, m;

V - el ancho de la abertura del troquel inferior, mm;

σb - Resistencia a la tracción del material, MPa.

La tabla de parámetros de fuerza de flexión recomendada por el fabricante también se calcula de acuerdo con la fórmula anterior.

El proceso de derivación y el ámbito de aplicación de la fórmula de cálculo de la fuerza de flexión.

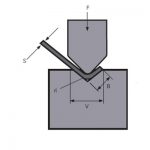
La Figura 1 es un diagrama esquemático del trabajo durante el doblado de láminas. A continuación se describe el proceso de derivación de la fórmula de cálculo de la fuerza de flexión y dos condiciones de parámetros adicionales. Primero, existen tales recomendaciones en el manual del producto. En el doblado libre, el ancho de abertura del troquel inferior seleccionado V es de 8 a 10 veces el espesor de la hoja S. Aquí tomamos la relación de aspecto .

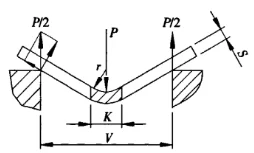
Figura 1 Diagrama esquemático de flexión.

P - fuerza de flexión

S - espesor de la hoja

V - ancho de apertura del troquel inferior

r - el radio interior cuando la hoja está doblada

K - el ancho de la proyección horizontal de la zona de deformación por flexión=9

En segundo lugar, el fabricante enumera los valores correspondientes del ancho del troquel V y el diámetro interior r de la pieza de trabajo de flexión en la tabla de parámetros de fuerza de flexión. Generalmente r=(0.16~0.17)V. Aquí, la relación diámetro-ancho =0.16.

Durante el proceso de doblado de la lámina de metal, el material en la zona de deformación se encuentra en un estado de deformación altamente plástico y se dobla en ángulo alrededor de la línea central. En la superficie exterior de la zona de flexión, en algunos casos pueden aparecer microfisuras. En la sección transversal de la zona de deformación, excepto en la vecindad de la capa central, las tensiones en otros puntos están cerca de la resistencia a la tracción del material. La parte superior de la capa neutra se comprime y la parte inferior se tensa. La figura 2 muestra una sección transversal y el correspondiente diagrama de tensiones en la zona de deformación.

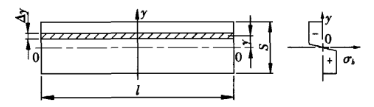
Figura 2 Diagrama de tensión

S - espesor de la hoja

l - longitud de doblado de la hoja

El momento de flexión en la sección transversal de la zona de deformación es:

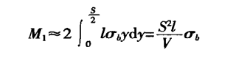
El momento de flexión generado por la fuerza de flexión de la máquina en la zona de deformación es (ver Figura 1):

Desde

Cuando se utilizan moldes de uso general para doblado libre en una máquina dobladora, la mayor parte de la hoja de metal se dobla 90°. Como se muestra en la Figura 3. K es:

Sustituyendo K en la ecuación (1), obtenemos:

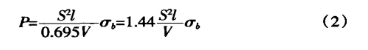
La resistencia a la tracción de los materiales ordinarios σb=450N/mm2, sustituyendo la fórmula (2) en:

Se puede ver del proceso de derivación que cuando se usa la ecuación (2) o la ecuación (3) para calcular la fuerza de flexión, los dos adicionales

deben cumplirse las condiciones de los parámetros mencionadas anteriormente. Es decir, la relación de aspecto=9, la relación diámetro-ancho=0.16, de lo contrario, causará un gran error.

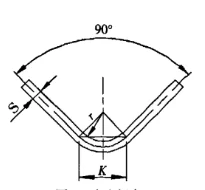
Figura 3 Flexión libre

S - espesor de la hoja

r - el radio interior cuando la hoja está doblada

K - el ancho de la proyección horizontal de la zona de deformación por flexión

Nuevos métodos y pasos para calcular la fuerza de flexión.

Debido a los requisitos de diseño o proceso, a veces es difícil cumplir los dos requisitos adicionales anteriores al mismo tiempo. En este momento, la fórmula de cálculo recomendada no debe usarse para calcular la fuerza de flexión, sino que debe realizarse de acuerdo con los siguientes pasos.

(1) De acuerdo con el grosor de la placa S, el radio de curvatura r y la abertura del troquel inferior V, se calculan respectivamente la relación entre el ancho y el grosor y la relación entre el diámetro y el ancho.

(2) Calcular el ancho de proyección de la zona de deformación según la deformación de la hoja.

(3) Aplique la fórmula (1) para calcular la fuerza de flexión.

En el proceso de cálculo se ha considerado la diferencia del radio de flexión y el cambio de la zona de deformación correspondiente. La fuerza de flexión calculada a partir de esto es más precisa y confiable que el resultado calculado por la fórmula generalmente recomendada. Ahora dé un ejemplo para ilustrar, como se muestra en la Figura 4.

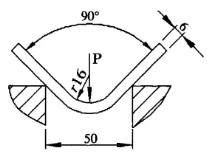
Figura 4 Nuevo método de cálculo

Conocido: El grosor de la lámina S=6 mm, la longitud de la lámina l=4 m, el radio de curvatura r=16 mm, el ancho de la abertura del troquel inferior V=50 mm y la resistencia a la tracción del material σb=450 N/mm2. Encuentre la fuerza de flexión requerida para la flexión libre.

Primero, encuentre la relación de aspecto y la relación diámetro-ancho:

En segundo lugar, calcule el ancho de proyección de la zona de deformación:

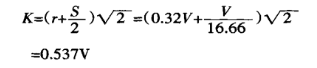
Finalmente, use la ecuación (1) para encontrar la fuerza de flexión:

Si se utiliza la fórmula habitual recomendada para calcular la fuerza de flexión:

Desde = 1.5, se puede ver que la diferencia entre los dos es 1.5 veces. La razón de este error es que el radio de flexión en este ejemplo es relativamente grande y el área de deformación correspondiente aumenta, por lo que se requiere una mayor fuerza de flexión durante la flexión. En este ejemplo, la relación diámetro-ancho = 0,32, que ha superado las condiciones adicionales de los parámetros introducidos anteriormente. Evidentemente, es inapropiado utilizar la fórmula normalmente recomendada para calcular la fuerza de flexión. Puede ver las ventajas del nuevo método de cálculo en este ejemplo.

Conclusión

Los pasos y las fórmulas para calcular la fuerza de flexión que se presentan aquí no solo se aplican al ángulo de flexión de la chapa, sino también al arco de flexión (estrictamente hablando, debería llamarse ángulo de flexión con un radio de flexión extra grande). Cabe señalar que la forma del molde es especial cuando la lámina se dobla en forma de arco. Al calcular la proyección de la zona de deformación, debe calcularse de acuerdo con los parámetros tecnológicos establecidos en el proceso tecnológico, que no se pueden expresar mediante una fórmula simple.

Al diseñar un molde en forma de arco, utilizando el método presentado en este artículo para calcular la fuerza de flexión, se pueden obtener resultados satisfactorios.